Wind bewirkt keinen Dopplereffekt.
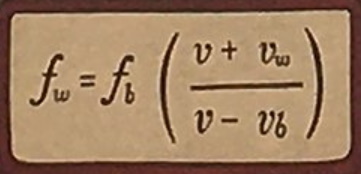 Noch kompakter gestaltet sich die Gesamtformel, wenn du die Bewegungsrichtungen im Vorzeichen von \(v_E\) und \(v_S\) hinterlegst.
In
Richtung der Schallwelle
vom Sender zum Empfänger
positiv und umgekehrt. Dann gilt
$$f_E=\frac{c - v_E}{c - v_S}\cdot f_S$$
$$\lambda_E=\frac{c - v_S}{c - v_E}\cdot \lambda_S$$
Ist \(v_S = v_E\), bewegen sich Sender und Empfänger also gleich schnell in die gleiche Richtung,
so
verschwindet der Dopplereffekt
\(f_E=f_S\)
. Dies ist beispielsweise der Fall, wenn sich das Medium bewegt:
Selbst hohe Windstärken bewirken keinen Dopplereffekt.
Noch kompakter gestaltet sich die Gesamtformel, wenn du die Bewegungsrichtungen im Vorzeichen von \(v_E\) und \(v_S\) hinterlegst.
In
Richtung der Schallwelle
vom Sender zum Empfänger
positiv und umgekehrt. Dann gilt
$$f_E=\frac{c - v_E}{c - v_S}\cdot f_S$$
$$\lambda_E=\frac{c - v_S}{c - v_E}\cdot \lambda_S$$
Ist \(v_S = v_E\), bewegen sich Sender und Empfänger also gleich schnell in die gleiche Richtung,
so
verschwindet der Dopplereffekt
\(f_E=f_S\)
. Dies ist beispielsweise der Fall, wenn sich das Medium bewegt:
Selbst hohe Windstärken bewirken keinen Dopplereffekt.