Mandelbrot-Menge - immer wieder Apfelmännchen
Mit Hilfe der Iterationsvorschrift
z → z2 + c
haben wir die Welt der
Julia-Mengen entdeckt.
Doch hinter dieser einfachen Formel schlummerte seit jeher ein weiteres Objekt von unglaublicher Komplexität im Verborgenen.
Erst 1979 wurde es von Benoit Mandelbrot sichtbar gemacht:
 Dabei ist es nicht schwer, dieses "Apfelmännchen" zu erzeugen.
Wir verwenden denselben Iterationsprozess wie bei den Julia-Mengen, jedoch mit folgender Bedingung:
Dabei ist es nicht schwer, dieses "Apfelmännchen" zu erzeugen.
Wir verwenden denselben Iterationsprozess wie bei den Julia-Mengen, jedoch mit folgender Bedingung:
Startpunkt z0 ist grundsätzlich der Ursprung 0 der komplexen Zahlenebene C.
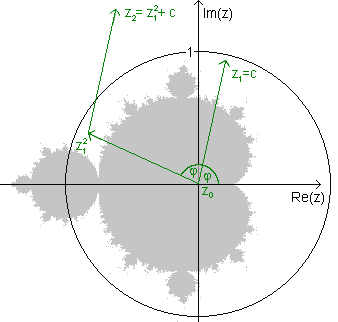
Die Mandelbrot-Menge M ist nun die Menge aller komplexen Zahlen c, für welche die Beträge der Folgezahlen
z1,
z2,
z3, ...
bei der Iteration
z → z2 + c nicht gegen ∞ streben.
M = {c ∈ C
| c → c2
+ c → ...
ist beschränkt}
M darf nicht mit einer Gefangenenmenge Gc verwechselt werden:
Gc = {z0 ∈ C
| z0 → z02
+ c → ...
ist beschränkt}
weiter


