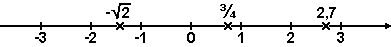
Einführung
Darstellung
Addition
Multiplikation

Wenn man nur mit ganzen Zahlen {…, -2, -1, 0, 1, 2, …} rechnet, stößt man bald auf ein Problem: Man kann zwar Gleichungen wie 4 · x = 20 lösen (die Lösung ist x = 5), doch bei 4 · x = 3 klappt das nicht mehr, denn diese Gleichung hat in den ganzen Zahlen keine Lösung.
Damit solche Gleichungen lösbar werden, muss man neue Zahlen einführen: die Bruchzahlen. Man definiert: ¾ ist die Zahl, die die Gleichung 4 · x = 3 löst.
Bruchzahlen und ganze Zahlen vereinigt nennt man rationale Zahlen.

Doch auch mit den rationalen Zahlen gibt es noch Probleme. Man kann zwar die Gleichung x² = 4 lösen (Lösung ist x = 2), aber x² = 2 hat in den rationalen Zahlen keine Lösung. Also müssen wieder neue Zahlen her: die irrationalen Zahlen. Und man definiert wieder: "die Wurzel aus 2" ist die Zahl, die die Gleichung x² = 2 löst.
Irrationale und rationale Zahlen vereinigt nennt man reelle Zahlen.

Die Gleichung x² = 2 kann man nun lösen, aber die Gleichung x² = -1 hat immer noch keine Lösung. Eine weitere Zahlbereichserweiterung liefert die imaginären Zahlen. Die wichtigste dieser imaginären Zahlen ist i, sie ist definiert als Lösung der Gleichung x² = -1.
Imaginäre und reelle Zahlen vereinigt nennt man komplexe Zahlen.

Alle komplexen Zahlen lassen sich als Summe einer reellen Zahl und einem Vielfachen von i darstellen:
z = a + b·i, wobei a und b reelle Zahlen sind.
a heißt Realteil von z (oder kurz Re(z)) und b Imaginärteil von z (Im(z)).

Alle reellen Zahlen lassen sich als Punkte auf einem Zahlenstrahl darstellen:

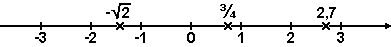
Bei komplexen Zahlen reicht ein Zahlenstrahl nicht mehr aus, man braucht jetzt eine Zahlenebene. Der Realteil einer komplexen Zahl wird auf der waagrechten, der Imaginärteil auf der senkrechten Achse abgetragen.

Der Abstand r einer Zahl z vom Ursprung 0 heißt Betrag von z, oder kurz abs(z), oder noch kürzer |z|. Es gilt (nach Pythagoras):

Beispiel: |9-5i|² = 9² + 5² = 81 + 25 = 106, also ist |9-5i| = √106 ≈ 10,3

Wenn man nur den Winkel φ (vgl. Zeichnung) und den Betrag einer Zahl z kennt, kann man mit trigonometrischen Funktionen den Real- und den Imaginärteil von z ausrechnen:

Also ist z = r · cos(φ) + r · sin(φ) · i = r · [cos(φ) + i · sin(φ)].

Die analytische Identität cos(φ) + i · sin(φ) = exp(iφ), wobei exp die Exponentialfunktion zur Basis e (Eulersche Zahl) ist, erlaubt eine weitere Darstellung komplexer Zahlen:

Man kann mit komplexen Zahlen fast genauso rechnen, wie mit reellen Zahlen. Dazu lässt man i einfach als Variable stehen. Die Addition zweier Zahlen z = a + b·i und w = c + d·i funktioniert also folgendermaßen:

Man kann also zwei komplexe Zahlen addieren, indem man ihre Realteile und ihre Imaginärteile einzeln addiert.

Beispiel: (3 + 7i) + (5 - 2i) = (3 + 5) + (7 - 2)i = 8 + 5i

Auch die Multiplikation lässt sich in gewohnter Weise durchführen:

Und weil wir i so definiert haben, dass i² = -1 ist, gilt

Beispiel: (3 + 7i) · (5 - 2i) = 3·5 - 7·(-2) + [3·(-2) + 7·5] · i = 15 + 14 + (-6 + 35)i = 29 + 29i

Man kann eine komplexe Zahl auch mit sich selbst multiplizieren, also quadrieren:

Beispiel: (5 - 2i)² = 5² - (-2)² + 2·5·(-2)·i = 25 - 4 + (-20)i = 21 - 20i

Mit der Eulerschen Schreibweise zeigt sich unter Anwendung von exp(a) · exp(b) = exp (a+b) eine elegante geometrische Interpretation für die Multiplikation zweier komplexer Zahlen:

Während sich die Radien der Zahlen multiplizieren, addieren sich ihre Winkel.

Beispiel: (4 exp(i·210°))² = 16 exp (i·60°)