zurück

Die folgende Abbildung zeigt jeweils die Bahnpunkte z1 (= c), z2, z3, ... (im Bild: 1, 2, 3, ...) der Iteration z  → z2 + c für vier verschiedene c (grün, blau, rot und schwarz):

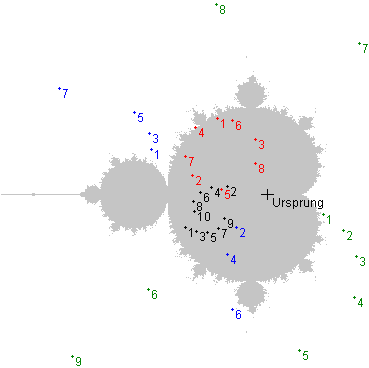Die Bahnen von c (im Bild: 1) und c verschwinden offensichtlich jeweils in der Unendlichkeit. Das bedeutet, c und c gehören nicht zu M. (Es gilt wie bereits festgestellt: Sobald ein Punkt zn weiter als 2 vom Ursprung entfernt ist, entkommt seine Bahn garantiert ins Unendliche, weil der Betrag aller folgenden Bahnpunkte mit jeder weiteren Iteration zunimmt.)
Anders bei c und c. Ihre Bahnen bleiben auf ein bestimmtes Gebiet beschränkt, also liegen c und c in M.

Das nächste Bild zeigt (blau) drei verschiedene c ∈ M, deren Bahnen jeweils spiralförmig einem Grenzwert zustreben. Zusätzlich sind (rot) die langsam ins Uendliche irrenden Folgepunkte eines c außerhalb M eingezeichnet.

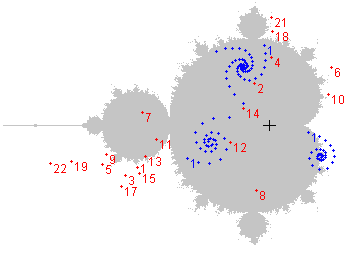Wer selbst mit solchen Orbits experimentieren möchte, kann das Applet "Iteration bei der Mandelbrotmenge" oder die Tabelle "Mandel" in folgender Arbeitsmappe verwenden:

weiter

Abb. aus www.fractal-dome.de