zurück
Betrachten wir die Bahnen einiger reeller c ∈ [-2;0,25] = M ∩
IR:
Die Werte sind auf 3 Dezimalen gerundet.
| zn |
c = -2 |
c = -1,99 |
c = -1,75 |
c = -1,3 |
c = -1,1 |
c = 0,25 |
| z0 |
0 |
0 |
0 |
0 |
0 |
0 |
| z1 |
-2 |
-1,99 |
-1,75 |
-1,3 |
-1,1 |
0,25 |
| z2 |
2 |
1,970 |
1,313 |
0,390 |
0,110 |
0,313 |
| usw. |
| z100 |
2 |
-0,839 |
-1,747 |
0,019 |
0,092 |
0,491 |
| z101 |
2 |
-1,286 |
1,303 |
-1,300 |
-1,092 |
0,491 |
| z102 |
2 |
-0,336 |
-0,052 |
0,389 |
0,092 |
0,491 |
| z103 |
2 |
-1,877 |
-1,747 |
-1,149 |
-1,092 |
0,491 |
| z104 |
2 |
1,532 |
1,303 |
0,019 |
0,092 |
0,491 |
| z105 |
2 |
0,358 |
-0,052 |
-1,300 |
-1,092 |
0,491 |
| z106 |
2 |
-1,862 |
-1,747 |
0,389 |
0,092 |
0,491 |
| z107 |
2 |
1,476 |
1,303 |
-1,149 |
-1,092 |
0,491 |
| z108 |
2 |
0,189 |
-0,052 |
0,019 |
0,092 |
0,491 |
Eine anschauliche Darstellung der Iterationsergebnisse reeller c zeigt untenstehendes Feigenbaum-Diagramm, dem wir (etwas abgewandelt) schon bei der Iteration der logistischen Gleichung begegnet sind. Hier sind die Zahlen z100 bis z200 als Ordinatenwerte über der Abszisse c aufgetragen. (Das Apfelmännchen ist zum Vergleich gestreckt abgebildet.)
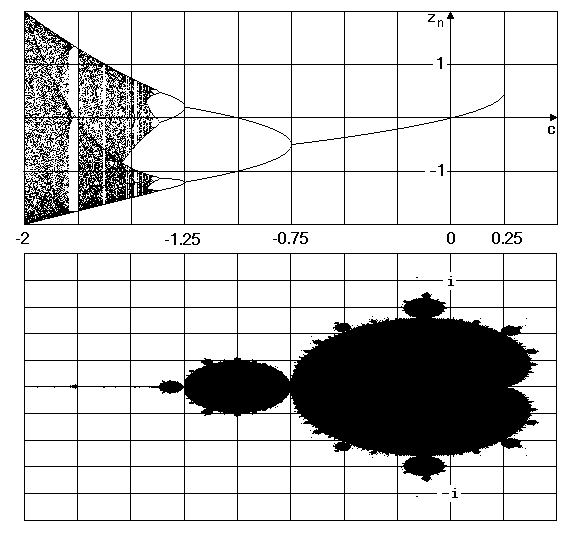
Feigenbaum-Diagramm der Iteration
z → z2 + c mit c ∈ [-2;0,25]
Wir stellen fest:
- c = -2: Wir befinden uns am äußersten linken Rand der "Antenne" des Apfelmännchens. Die Iteration bleibt auf der 2 festgenagelt. 2 ist ein Fixpunkt.
- c = -1,99: Die Bahnpunkte variieren chaotisch.
- c = -1,75: Im Mini-Apfelmännchen der Antenne ist eine Insel der Ordnung. Die Bahnpunkte pendeln sich in einem 3er-Zyklus ein.
- c = -1,3: In der kleinen "Knospe" haben die Bahnpunkte die Periode 4.
- c = -1,1: Die nächstgrößere Kugelknospe beinhaltet Bahnen der Periode 2.
- c = 0,25: Am rechten reellen Ende des Apfelmännchens strebt die Iteration einem Grenzwert zu.
weiter

