Feigenbaum-Diagramm - Aus eins mach' zwei
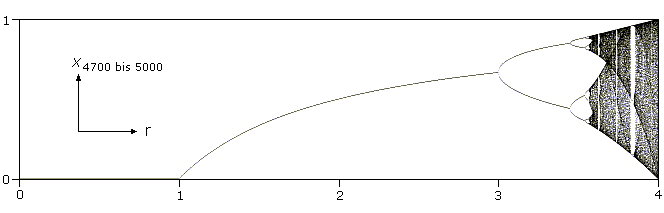
Unsere bewährte Tabelle zur Iteration der logistischen Gleichung liefert bei steigender Periode keine sehr übersichtlichen Ergebnisse. Man kann nicht sicher einen 16er-Zyklus von einem sich einpendelnden 8er-Zyklus unterscheiden. Der Physiker Mitchell Feigenbaum hatte an dieser Stelle die Idee für eine weitere Computerdarstellung des Iterations-Szenarios: Wir (bzw. der Computer) iterieren irgendein x0 für festes r, sagen wir 4700-mal. x4700 dürfte dann schon am Attraktor kleben. Dann tragen wir die folgenden, sagen wir 300, Iterationsergebnisse x4700 bis 5000 als Ordinatenwert über der Abszisse r in ein Diagramm ein. Dies wiederholen wir für alle 0 ≤ r ≤ 4. Vor unseren Augen entsteht ein Feigenbaum-Diagramm:
 Wir erkennen die bereits festgestellten Phänomene wieder:
Wir erkennen die bereits festgestellten Phänomene wieder:
- 0 ≤ r ≤ 1: Die Population stirbt aus.
- 1 < r ≤ 3: Die Populationsgröße nimmt (praktisch) den Attraktorwert pr = 1 - 1/r an.
- 3 < r ≤ 4: Die Populationsgröße schwankt in einem 2er-, 4er-, 8er-, usw. Zyklus bis zu einem gewissen Punkt auf der r-Achse. Was ist jetzt los? Die Ordinatenwerte xn hüpfen ziellos auf und ab, d.h. die Populationsgröße variiert von Jahr zu Jahr völlig unregelmäßig, bis schließlich bei r = 4 alle möglichen Populationszahlen von 0 bis 1 auftreten. Das Chaos ist ausgebrochen! Wir müssen dieses Tohuwabohu mit FBAUM im wahrsten Sinne des Wortes unter die Lupe nehmen:

zum Kapitel "Sensitivität"


