Entdeckt wurde die Mandelbrot-Menge M bei Untersuchungen zu Juliamengen J_c. Diese kann man in zwei Schubladen stecken: Entweder ist J_c (und damit auch die Gefangenenmenge G_c) ein zusammenhängendes Gebiet oder eine total unzusammenhängende Punktwolke. Zur besseren Übersicht markierte man alle Punkte c der komplexen Zahlenebene, für die J_c zusammenhängend ist. Das war die Geburtsstunde von M. Es gilt:

M = {c ∈ C | J_c ist zusammenhängend}

	c = 0,15 + 0i ∈ M
	c = 0,25 + 0i ∈ M
	c = 0,26 + 0i ∉ M
	c = 0,50 + 0i ∉ M

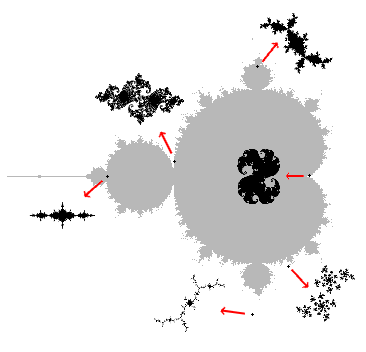
Ebenso zerfallen Gefangenenmengen bei Variation von c entlang eines aus M führenden Pfads zu Staub. Während auf dem ersten Bild für c ∈ M eine zusammenhängende Gefangenenmenge Gc zu sehen ist, löst sich diese immer mehr auf, bis schließlich auf dem letzten Bild für c ∉ M getrennte Bereiche zu erkennen sind. M selbst ist übrigens zusammenhängend. Man findet also immer eine Straße zwischen zwei Punkten aus M, die vollständig in M liegt. Die Komplexität von M offenbart sich erst bei Vergrößerungen des Randes, die bei Anwendung von Färbungs-Algorithmen verblüffende Gebilde präsentieren. Beispiele zeigt die Bildergalerie.

Abb. 1 u. 3 aus www.fractal-dome.de