Iteration der logistischen Gleichung - attraktive Zahlen

Freilich sehen wir ein, dass die realistischen Populationsverhältnisse komplizierter liegen, als dass sie allein durch das logistische Modell xn+1 = r·(1-xn)·xn exakt erfasst werden könnten. Uns interessieren jedoch im folgenden mehr die mathematischen Geheimnisse, die in dieser Formel verborgen liegen.

Zwei Parameter müssen wir vor der Iteration festlegen:
  • Startwert x0 ∈ [0;1]
  • Parameter r ∈ [0;4]
Dann kann's losgehen. Hier sieht man ein Beispiel für x0 = 0,09 und r = 3,54.
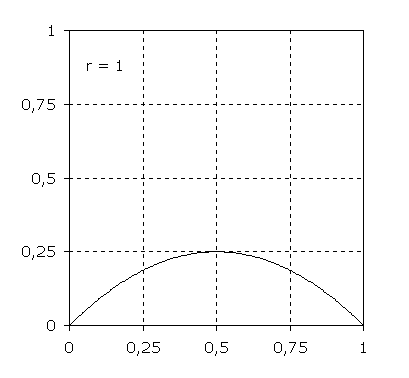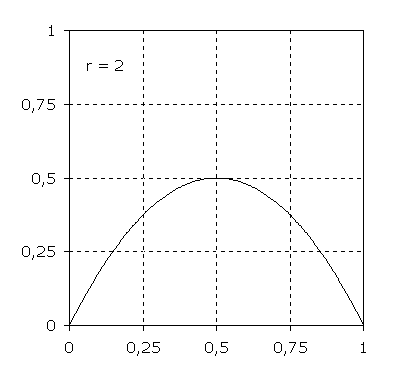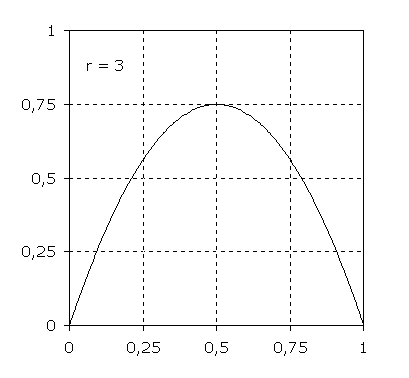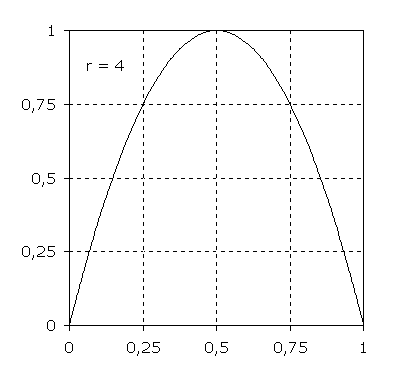
Graphen der Funktion

f: x → r·(1-x)·x; D = [0;1]

für verschiedene Parameter r. Der Wertebereich ist für 0 ≤ r ≤ 4 Teilmenge des Intervalls [0;1]. Die nach unten geöffneten Parabeln enthalten unabhängig von r die Punkte (0|0) und (1|0). Die Scheitel liegen bei (0,5|r/4).
Auf den Kurven dieser Funktionenschar liegen alle Punkte der Form (xn|xn+1). 		Iterationsfunktion (c) C. Wolfseher
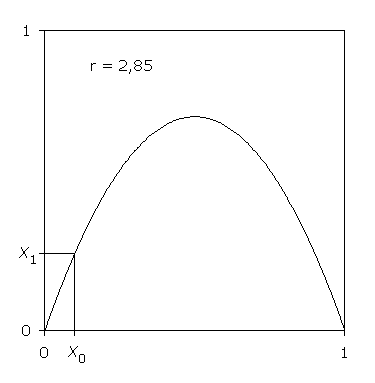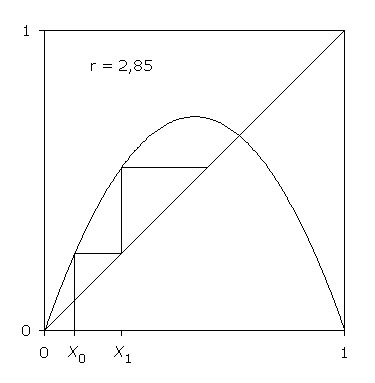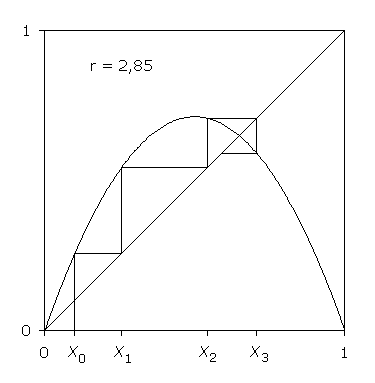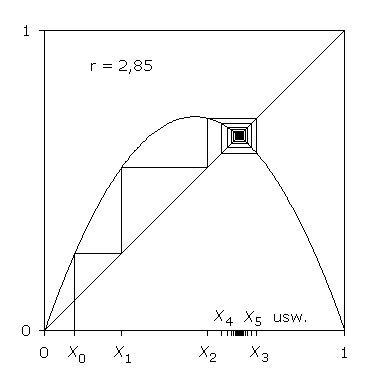
grafische Iteration für x=0,1 und r=2,85 (c) C. Wolfseher Die graphische Iteration ist eine aufschlussreiche Veranschaulichung der Entwicklung der Zahlenfolge. Mit Hilfe des Graphen der Iterationsfunktion kann der auf x0 folgende Wert x1 als Kurvenordinate ermittelt werden. Dieser wird an der Winkelhalbierenden auf die Abszisse gespiegelt und ist dort Ausgangspunkt der nächsten Iteration.
Mit der folgenden Tabelle kann man die Iteration der logistischen Gleichung xn+1 = r·(1-xn)·xn zunächst rein experimentell untersuchen. Es werden die numerische Folge, der Orbit und die graphische Iteration gezeigt.

weiter