7. Aus ein mach um | Berechnung der Kreiszahl π

Um sicher zu gehen, dass die Umfänge $u_n$ für wachsende Eckenzahl $n$ wirklich gegen den Kreisumfang $U_K=\pi$ und nicht einen kleineren Wert streben, müssen wir $U_K$ auch von der anderen Seite mit umbeschriebenen Tangentenvielecken in die Mangel nehmen.

Man kann nun analog zum Sehnenvieleck zeigen, dass der Umfang $U_n$ der umbeschriebenen $n$-Ecke mit wachsendem $n$ schrumpft, jedoch stets größer als der Kreisumfang $U_K$ ist.

Das umbeschriebene $n$-Eck erhält man aus dem einbeschriebenen $n$-Eck durch eine Streckung mit dem Zentrum $M$ und dem Streckfaktor $m$ und es gilt $U_n=m \cdot u_n$.

• Berechne den Streckfaktor $m$!

$$\begin{align} m &=\frac{r}{\overline{MF}}\\ &=\cssId{Step1}{\frac{r}{\sqrt{r^2-\left(\frac{s_n}{2}\right)^2}}}\\ &=\cssId{Step2}{\frac{\frac{1}{2}}{\sqrt{\left(\frac{1}{2}\right)^2-\left(\frac{s_n}{2}\right)^2}}}\\ &=\cssId{Step3}{\frac{\frac{1}{2}}{\frac{1}{2}\cdot\sqrt{1-s_n^2}}}\\ &=\cssId{Step4}{\underbrace{\frac{1}{\sqrt{1-s_n^2}}}_{\to 1 \text{ für } n \to \infty}}\\ \end{align}$$

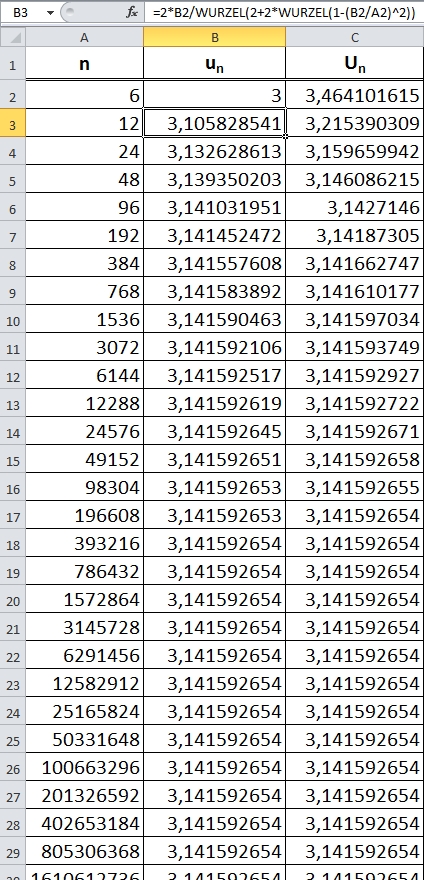
Mit wachsender Eckenzahl $n$ wird die Seitenlänge $s_n$ beliebig klein und damit strebt $m$ gegen 1. $U_n$ und $u_n$ sind dann nicht mehr unterscheidbar. Die Länge der Intervalle $\left[u_n;U_n\right]$ wird also beliebig klein und mittendrin steckt $U_K=\pi$. Zusammenfassung Sind $u_6, u_{12}, u_{24}, \ldots$ die Umfänge der einbeschriebenen und $U_6, U_{12}, U_{24}, \ldots$ die Umfänge der umbeschriebenen regelmäßigen Vielecke eines Kreises mit dem Radius $r=\frac{1}{2}$ LE, so ist $$\left[u_6;U_6\right], \left[u_{12};U_{12}\right], \left[u_{24};U_{24}\right], \ldots$$ eine Intervallschachtelung für die Kreiszahl $\pi$.

«    •    »