n Xn=r*(1-x)*x Xn=r*x-r*sqr(x) 13266 0.03255742746 0.03255742746 13267 0.12598976549 0.12598976549 13268 0.44046537793 0.44046537793 13269 0.98582251510 0.98582251510 13270 0.05590593529 0.05590593529 13271 0.21112184676 0.21112184677 13272 0.66619765032 0.66619765035 13273 0.88951336411 0.88951336407 13274 0.39311735672 0.39311735684 13275 0.95430440226 0.95430440236 13276 0.17443004035 0.17443003998 13277 0.57601680550 0.57601680454 13278 0.97688578112 0.97688578171 13279 0.09031980705 0.09031980481 13280 0.32864855802 0.32864855068 13281 0.88255473332 0.88255472327 13282 0.41460750405 0.41460753482 13283 0.97083248654 0.97083250756 13284 0.11326707847 0.11326699928 13285 0.40175058962 0.40175034462 13286 0.96138821344 0.96138802087 13287 0.14848366601 0.14848437678 13288 0.50574506775 0.50574706652 13289 0.99986797679 0.99986788491 13290 0.00052802314 0.00052839056 13291 0.00211097731 0.00211244546 13292 0.00842608434 0.00843193214 13293 0.03342034176 0.03344333864 13294 0.12921369005 0.12929952698 13295 0.45007004941 0.45032463721 13296 0.99002800014 0.99012943332 13297 0.03949023632 0.03909255435 13298 0.15172303023 0.15025730619 13299 0.51481260930 0.51072019252 13300 0.99912234642 0.99954030989 13301 0.00350753321 0.00183791518 13302 0.01398092168 0.00733814900 13303 0.05514182202 0.02913720229 13304 0.20840480594 0.11315290294 13305 0.65988897120 0.40139729399 13306 0.89774206756 0.96111002547 13307 0.36720499077 0.14951017765 13308 0.92946194210 0.50862753771 13309 0.26224976116 0.99970226237 13310 0.77389929573 0.00119059592 13311 0.69991670320 0.00475671361 13312 0.84013324713 0.01893634914 13313 0.53723749679 0.07431105530 13314 0.99445347533 0.27515568943 13315 0.02206304293 0.79778014401 13316 0.08630506027 0.64530794332 13317 0.31542598737 0.91554240643 13318 0.86372973545 0.30929803384 13319 0.47080271820 0.85453104041 13320 0.99659007494 0.49723096553
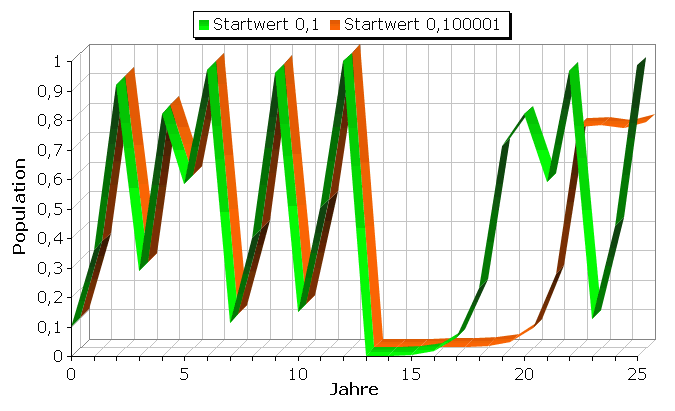
Es geht noch weiter: Wir verwenden denselben Computer mit derselben Rechengenauigkeit und derselben Iterationsformel, starten jedoch mit um 1/1000000 verschiedenen Anfangswerten. Das wären bei einer Million Schwammspinnern nur ein Falter mehr! Das Ergebnis (vgl. Tabelle unten) spricht für sich.
n Xn Xn 0 0.10000100000 0.10000000000 1 0.36000320000 0.36000000000 2 0.92160358395 0.92160000000 3 0.28900167199 0.28901376000 4 0.82191882230 0.82193922612 5 0.58547308739 0.58542053874 6 0.97077740533 0.97081332624 7 0.11347453853 0.11333924733 8 0.40239227054 0.40197384937 9 0.96189092460 0.96156349517 10 0.14662709511 0.14783655969 11 0.50051036034 0.50392364525 12 0.99999895813 0.99993842003 13 0.00000416748 0.00024630470 14 0.00001666985 0.00098497615 15 0.00006667827 0.00393602390 16 0.00026669529 0.01568212646 17 0.00106649666 0.06174478947 18 0.00426143698 0.23172948176 19 0.01697310854 0.71212371618 20 0.06674008852 0.82001411614Dabei liegen die Resultate nicht knapp nebeneinander. Sie zeigen vielmehr keinerlei Korrelation. Der Grund für diese chaotischen Ergebnisse ist zunächst in der beschränkten Rechengenauigkeit eines jeden Computers zu suchen. Bereits nach wenigen Iterationen muss der Rechner Nachkommastellen abschneiden. Diese Rundungsfehler pflanzen sich dann von Iterationsschritt zu Iterationsschritt fort.
Doch ist es nicht damit erledigt, die Schuld für die unterschiedlichsten Ergebnisse bei (fast) identischer Rechnung nur dem dummen Computer zuzuweisen. Schließlich stimmten die für 0 < r < r∞ computerberechneten Werte perfekt mit der Theorie überein. Auch sonst leisten Rechner in der Wissenschaft zuverlässige Arbeit. Mit kleinen Rundungsfehlern kann man leben.
Die Tücke des Objekts steckt in der logistischen Gleichung. Während links von r∞ die Ordnung triumphiert und jegliche Fehler und Schwankungen glattbügelt, hat rechts von r∞ Chaos die Vorherrschaft übernommen. Winzigste Ungenauigkeiten und unvermeidliche, nicht mehr registrierbare Messfehler in den Startwerten führen langfristige Vorausberechnungen ad absurdum. Das System ist sensitiv abhängig von den Anfangsbedingungen.
Sicher ist der Orbit eines theoretisch exakt bestimmten x0 durch den Iterator exakt festgelegt (das schwache Kausalitätsprinzip ist zu keiner Zeit verletzt), aber eben nicht (auf lange Zeit) berechenbar! Man spricht vom deterministischen Chaos.
